1. Partitional Clustering v.s. Hierarchical Clustering
- Partitioning clustering: A division of data objects into non-overlapping subsets (clusters) such that each data object is in exactly one subset.
- Hierarchical clustering: A set of nested clusters organized as a hierarchical tree.
2. Types of Cluster
- Well-Separated Clusters: a cluster is a set of points such that any point in a cluster is closer (or more similar) to every other point in the cluster than any point not in the cluster.
- Center-based Clusters: A cluster is a set of objects such that any point in a cluster is closer (more similar) to the "center" of a cluster, than to the center of any other cluster.
- The center of a cluster is often a centroid, the average of all the points in the cluster, or a medoid, the most "representative" point of a cluster.
- Contiguous Clusters (Nearest Neighbor or Transitive): A cluster is a set of points such that a point in a cluster is closer (or more similar) to one or more other points in the cluster than to any point not in the cluster.
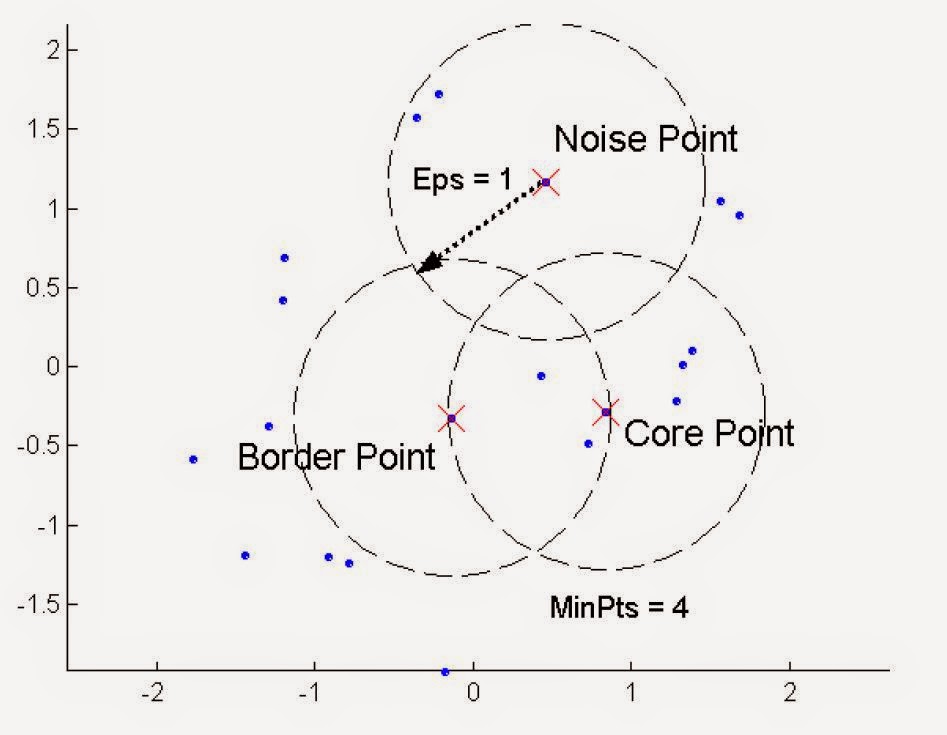
- Density-based: A cluster is a dense region of points, which is separated by low-density regions, from other regions of high density.
- Used when cluster are irregular or intertwined.
- Shared Property or Conceptual Clusters: Finds clusters that share some common property or represent a particular concept.

- Cluster Defined by an Objective Function:
- Finds clusters that minimize or maximize an objective function
- Enumerate all possible ways of dividing points into clusters and evaluate the "goodness" of each potential set of clusters by using the given objective function (NP hard).
- Can have global or local objectives
- hierarchical clustering algorithms typically have local objectives
- partitional algorithms typically have global objectives
- A variant of the global objective function approach is to fit the data to a parameterized model
- parameters for the model are determined from the data
- mixture models assume that the data is a "mixture" of a number of statistical distributions.
- Map the clustering problem to a different domain and solve a related problem in that domain
- proximity matrix defines a weighted graph, where the nodes are the points being clustered, and the weighted edges represent the proximities between points.
- Clustering is equivalent to breaking the graph into connected components, one for each cluster.
3. K-means Clustering
- Initial centroids are often chosen randomly.
- Clusters produced vary from one run to another.
- The centroid is (typically) the mean of the points in the cluster.
- "Closeness" is measured by Euclidean distance, cosine similarity, correlation, etc.
- K-means will converge for common similarity measures mentioned above.
- Most of the converge happens in the few iterations.
- often the stopping condition is changed to "until relatively few points change clusters"
- Complexity is O(n*k*i*d)
- n: number of points
- k: number of clusters
- i: number of iterations
- d: number of attributes
4. Evaluating K-means Clustering
- Most common measure is Sum of Squared Error (SSE)
- for each point, the error in the distance to the nearest cluster
- to get SSE, we square these errors and sum them
- SSE = $\sum^k_{i=1} \sum_{x \in C_i}$ dist^2$(m_i,x)$
- where x is the data point in cluster $C_i$ and $m_i$ is the representative point for cluster $C_i$
5. Problem with Selecting Initial Points
- If there are K "real" clusters then the chance of selecting one centroid from each cluster is small
- Chances is relatively small when K is large.
- If clusters are the same size, n, then
- P = $\frac{ \mbox{number of ways to select one centroid from each cluster}}{\mbox{number of ways to select K centroids}} = \frac{K!n^K}{(Kn)^K} = \frac{K!}{K^K}$
- Solutions to Initial Centroids Problem
- Multiple runs: helps, but probability is not on your side
- Sample and user hierarchical clustering to determine initial centroids
- Select more than k initial centroids and then select among these initial centroids
- select most widely separated
- Postprocessing
- Bisecting K-means
- Not as susceptible to initialization issues
6. Handling Empty Clusters
- Basic K-means algorithm can yield empty clusters
- Several strategies
- Choose the point that contributes most to SSE
- Choose a point from the cluster with the highest SSE
- If there are several empty clusters, the above can be repeated several times
7. Updating Centers Incrementally
- In the basic K-means algorithm, centroids are updated after all points are assigned to a centriod
- An alternative is to update the centriods after each assignment (incremental approach)
- each assignment updates zero or two centroids
- more expensive
- introduces an order dependency
- never get an empty cluster
- can use "weights" to change the impact
8. Pre-processing and Post-processing
- Pre-processing
- normalize the data
- eliminate outliers
- Post-processing
- Eliminate small clusters that may represent outliers
- Split "loose" clusters, i.e., clusters with relatively high SSE
- Merge clusters that are "close" and that have relatively low SSE
- Can use these steps during the clustering process
9. Bisecting K-means
- Bisecting K-means algorithm
- variant of K-means that can produce a partitional or a hierarchical clustering
10. Limitations of K-means
- K-means has problems when clusters are of differing
- sizes
- densities
- non-globular shapes
- K-means has problems when the data contains outliers.
- One solution is to use many clusters
- find parts of clusters, but need to put together