Markov Chain - Classifications of States

1. Definition of States

• Communicate: State i and j communicate ($i \leftrightarrow j$) if i is reachable from j and j is reachable from i. (Note: a state i always communicates with iteself)
• Irreducible: a Markov chains is irreducible if all states are in the same communication class.
• Absorbing state: $p_(ii) = 1$
• Closed Set: a set of states S is a closed set if no state outside of S is reachable from any state in S. (This is like absorbing set of states)
• $f_i$: be the probability that, starting in state i, the process returns (at some point) to the sate i
• Transient: a state is transient if $f_i < 1$
• Recurrent: a state that is not transient is recurrent, i.e., $f_i =1$. There are two types of reurrent states
• Positive recurrent: if the expected time to return to the state if finite
• Null recurrent: if the expected time to return to the sate i is infinite (this requires an infinite number of states)
• Periodic: a state is i period if $k>1$ where k is the smallest number such that all paths leading from state i back to state i has a multiple of k transitions
• Aperiodic: if it has period k =1
• Ergodic: a state is ergodic if it is positive recurrent and aperiodic.

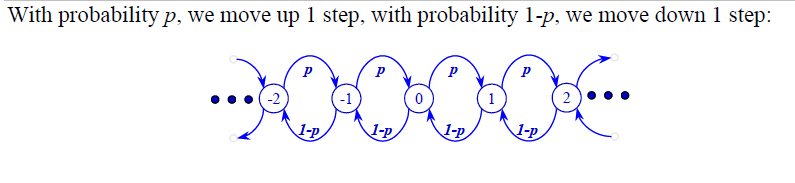
2. Example: Gambler's Ruin

3. Example: Random Walk