- Stochastic Process course notes
1. Definition
- Probability function: $f(x) = \lambda e^{-\lambda x}$, $x \geq 0$
- Cumulative Distribution Function (CDF): $F(x) = 1-e^{-\lambda x}$, $x \geq 0$
- Complement of the CDF (CCDF): $F^c(x) = e^{-\lambda x}$, $x \geq 0$.
2. Memoryless Property
Def`1: A random variable X has the memoryless property if $Pr\{X>t+s| X>s\} = Pr\{X>t\}$
Def`2: A random variable X has the memoryless property if $Pr\{X>t+s\} = Pr\{X>t\} Pr\{X>s\}$
The exponential distribution is the only distribution that has the memoryless property (Satisfy definition 2)
Then what is the probability that $X_1 < X_2$.
More generally
$Pr\{X_i = min[X_1,\cdots, X_n]\} = \frac{\lambda_i}{\lambda_1+\lambda_2+\cdots +\lambda_n}$
Def`2: A random variable X has the memoryless property if $Pr\{X>t+s\} = Pr\{X>t\} Pr\{X>s\}$
The exponential distribution is the only distribution that has the memoryless property (Satisfy definition 2)
3. Useful Properties: First occurrence among events
Assume $X_1, X_2, \cdots, X_n$ are exponential variable with rate $\lambda_1, \lambda_2, \cdots, \lambda_n$.Then what is the probability that $X_1 < X_2$.
More generally
$Pr\{X_i = min[X_1,\cdots, X_n]\} = \frac{\lambda_i}{\lambda_1+\lambda_2+\cdots +\lambda_n}$
4. Distribution of time of first event
This is the CDF of an exponential RV with rate $(\lambda_1 + \lambda_2)$, therefore
$min(X_1, X_2)$ ~ $exp(\lambda_1 + \lambda_2)$
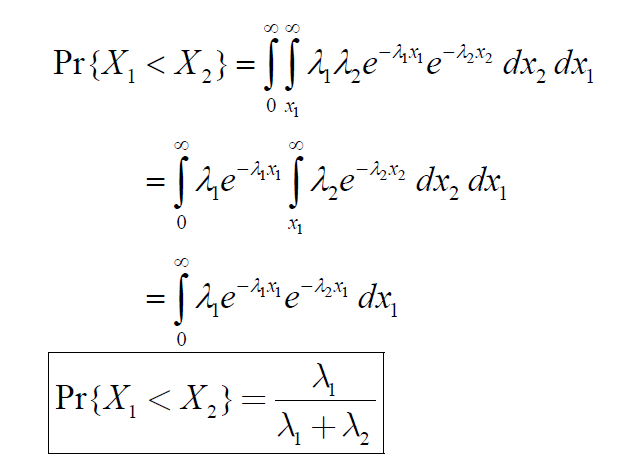


No comments:
Post a Comment